elementos de una elipse
La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:
- El semieje mayor (el segmento C-a de la figura), y
- el semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor respectivamente.
Puntos de una elipse
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor, (PF1 + PF2 = 2a).
Si F1 y F2 son dos puntos de un plano, y 2a es una constante mayor que la distancia F1F2, un punto P pertenecerá a la elipse si se cumple la relación:
donde  es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.
 es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.
Ejes de una elipse
El eje mayor 2a, es la mayor distancia entre dos puntos adversos de la elipse. El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos adversos de la elipse. Los ejes de la elipse son perpendiculares entre si.
Excentricidad de una elipse
La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y uno.
 , con
, con 
Dado que 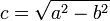 , también vale la relación:
, también vale la relación:
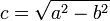 , también vale la relación:
, también vale la relación:
o el sistema:
La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero.3 La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.
(No se debe usar la letra e para designarla, porque se reserva para la base de los logaritmos naturales o neperianos. Véase: número e).
Excentricidad angular de una elipse
La excentricidad angular α es el ángulo para el cual el valor de la función trigonométrica seno concuerda con la excentricidad  , esto es:
, esto es:
 , esto es:
, esto es:
Constante de la elipse
En la figura de la derecha se muestran los dos radio vectores correspondientes a cada punto P de una elipse, los vectores que van de los focos F1y F2 a P. Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una una cantidad constante igual a la longitud 2a del eje mayor:
- PF1 + PF2 = 2a
En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.
Directrices de la elipse
Cada foco F de la elipse está asociado con una recta paralela al semieje menor llamada directriz (ver ilustración de la derecha). La distancia de cualquier punto P de la elipse hasta el foco F es una fracción constante de la distancia perpendicular de ese punto P a la directriz que resulta en la igualdad:
La relación entre estas dos distancias es la excentricidad  de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
 de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
de la elipse. Esta propiedad (que puede ser probada con la herramienta esferas de Dandelin) puede ser tomada como otra definición alternativa de la elipse.
|
Además de la bien conocida relación  , también es cierto que
, también es cierto que  , también es útil la fórmula
, también es útil la fórmula  .
.
 , también es cierto que
, también es cierto que  , también es útil la fórmula
, también es útil la fórmula  .
.
Aunque en la figura solo se dibujó la directriz del foco derecho, existe otra directriz para el foco izquierdo cuya distancia del centro O es -d, la cual además es paralela a la directriz anterior.
Ecuaciones de la elipse
En coordenadas cartesianas
Forma cartesiana centrada en origen
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Forma cartesiana centrada fuera del origen
Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:
En coordenadas polares
Forma polar centrada en origen
En coordenadas polares, con origen en su centro, la ecuación de la elipse es:
(epc 1)
Una ecuación más elegante que la anterior (pero que obliga a pre-calcular la excentricidad  ), es:
), es:
 ), es:
), es:(epc 2)
Para ambas ecuaciones a es el semieje mayor, b es el semieje menor de la elipse, θ es el ángulo polar y para la () ε es la excentricidad.
Si no se quiere pre-calcular la excentricidad  convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
 convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
convendrá utilizar la ecuación (), en caso contrario utilizar la ecuación ().
Formas polares centradas en un foco
En coordenadas polares, con el origen en uno de sus focos, la ecuación de la elipse es:
(501)
Para el otro foco:
(502)
En el caso un poco más general de una elipse con un foco en el origen y el otro foco en la coordenada angular φ, la forma polar es:
(503)}
El ángulo θ de las ecuaciones (),() y () es la llamada anomalía verdadera del punto y el numerador de las mismas a(1 − ε2) es el llamadosemi-latus rectum de la elipse, normalmente denotado l. El semi-latus rectum es la distancia entre un foco y la misma elipse sobre una línea perpendicular al semieje mayor que pasa por el foco.
Formas paramétricas
La ecuación paramétrica de una elipse con centro en (h,k) y siendo a el semieje mayor y b el menor, es:
con 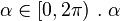 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
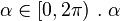 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es-
 .
.
La ecuación paramétrica de una elipse con centro en (h,k) en la que el parámetro θ sea concordante con el ángulo polar respecto al centro desplazado (h,k) es:
con  . El parámetro θ es el ángulo de un sistema polar cuyo origen está centrado en (h,k).
. El parámetro θ es el ángulo de un sistema polar cuyo origen está centrado en (h,k).
 . El parámetro θ es el ángulo de un sistema polar cuyo origen está centrado en (h,k).
. El parámetro θ es el ángulo de un sistema polar cuyo origen está centrado en (h,k).
Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.4
Longitud de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan ideó una ecuación más simple que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su fórmula, entre otros valores utiliza el “semieje mayor” y el “semieje menor”. Ecuación de la longitud de una elipse:
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.








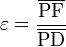

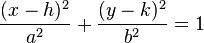

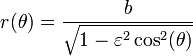

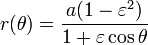





![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](http://upload.wikimedia.org/wikipedia/es/math/d/3/4/d34a512a10d8825e517cf922f7fca13c.png)
No hay comentarios:
Publicar un comentario