Propiedades geométricas
Aunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico:
|
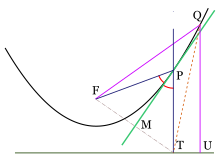
De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como distancia focal o radio focal.
Lado recto
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.
|
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.
Semejanza de todas las parábolas
Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
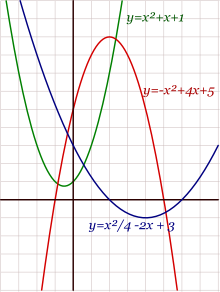
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.
Tangentes a la parábola
|
En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.
Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, sto quiere decir que MP es la tangente de la parábola en P.
Ecuaciones de la parábola
Con el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y=ax2 donde el parámetro aespecifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio,2 y se bosquejará a continuación usando notación moderna.
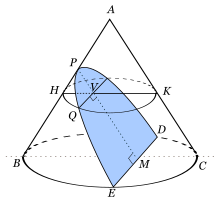
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QVperpendicular al eje. (QV corresponde al valor x en la versión analítica y PV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C.
Por el teorema de potencia de un punto:
.
Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:
.
Usando nuevamente los paralelismos:
.
Despejando HV y VK para sustituir en la fórmula de QV² resulta en
.
Pero el valor de  es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendo
 es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendo
arroja la expresión moderna y=ax².
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.
|
agrupando los términos y reordenando se obtiene una forma equivalente:
|
Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:
|
Ecuación involucrando la distancia focal
Pueden haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación. Sin embargo, dados dos puntos fijos, existe sólo una parábola que los tiene por vértice y foco ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.
Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p. Con esta configuración se tiene:
|
De forma alterna:
|
Es de notar que el coeficiente 4p es precisamente la longitud del lado recto de la parábola.
Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La ecuación de una parábola que se abre hacia abajo es similar excepto que varía un signo. En este caso, el foco sería (0,-p) y de esta forma:
|
Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar intercambiando los roles de x, y:
|
obteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.
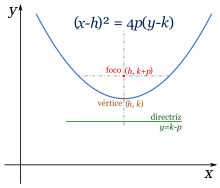
Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante una traslación. En el caso común de la parábola vertical hacia arriba se tiene
|
mientras que para la parábola horizontal se intercambia x con y:.
|
Ecuación general de una parábola
Hasta ahora se han descrito parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x ó de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.
|
Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma
 , donde a es distinto de cero.
, donde a es distinto de cero.







 .
.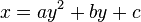 .
.
 .
. .
.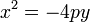 .
. ,
, ,
,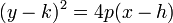 .
.

Best bets for soccer today - Sports Toto
ResponderEliminarToday, we're going to tell communitykhabar you 바카라 사이트 a few key to 토토사이트 checking into soccer 1xbet korean betting apps. herzamanindir.com/ of the most popular soccer betting options and which ones will